While cameras are incredibly useful for autonomous vehicles (such as in traffic sign detection and classification), other sensors also provide invaluable data for creating a complete picture of the environment around a vehicle. Because different sensors have different capabilities, using multiple sensors simultaneously can yield a more accurate picture of the world than using one sensor alone. Sensor fusion is this technique of combining data from multiple sensors. Two frequently used non-camera-based sensor technologies used in autonomous vehicles are radar and lidar, which have different strengths and weaknesses and produce very different output data.
Radars exist in many different forms in a vehicle: for use in adaptive cruise control, blind spot warning, collision warning, collision avoidance, to name a few. Radar uses the Doppler effect to measure speed and angle to a target. Radar waves reflect off hard surfaces, but can pass through fog and rain, have a wide field of view and a long range. However, their resolution is poor compared to lidar or cameras, and they can pick up radar clutter from small objects with high reflectivity. Lidars use infrared laser beams to determine the exact location of a target. Lidar data resolution is higher than radar, but lidars cannot measure the velocity of objects, and they are more adversely affected by fog and rain.

Example of lidar point cloud

Example of radar location and velocity data
A very popular mechanism for object tracking in autonomous vehicles is a Kalman filter. Kalman filters uses multiple imprecise measurements over time to estimate locations of objects, which is more accurate than single measurements alone. This is possible by iterating between estimating the object state and uncertainty, and updating the state and uncertainty with a new weighted measurement, with more weight being given to measurements with higher precision. This works great for linear models, but for non-linear models (such as those which involve a turning car, a bicycle, or a radar measurement), the extended Kalman filter must be used. Extended Kalman filters are considered the standard for many autonomous vehicle tracking systems.
I created an extended Kalman filter implementation which estimates the location and velocity of a vehicle with noisy radar and lidar measurements.
Exploring my implementation
All of the code and resources used in this project are available in my Github repository. Enjoy!
Technologies Used
- C++
- uWebSockets
- Eigen
Kalman filters
Conceptually, Kalman filters work on the assumption that the actual or “true” state of the object (for instance, location and velocity) and the “true” uncertainty of the state may not be knowable. Rather, by using previous estimates about the object’s state, knowledge of how the object’s state changes (what direction it is headed and how fast), uncertainty about the movement of the vehicle, the measurement from sensors, and uncertainty about sensor measurements, an estimate of the object’s state can be computed which is more accurate than just assuming the values from raw sensor measurements.
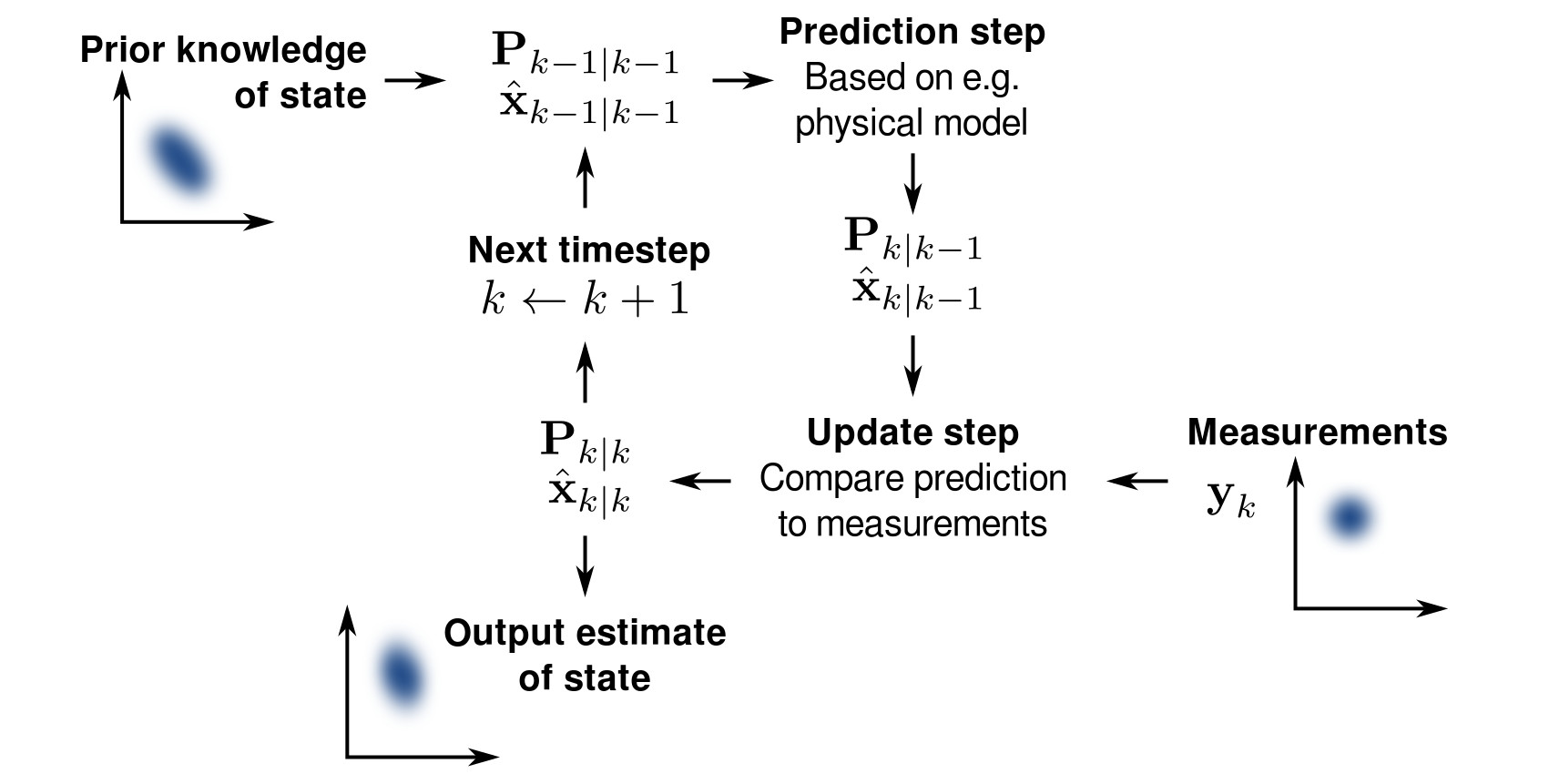
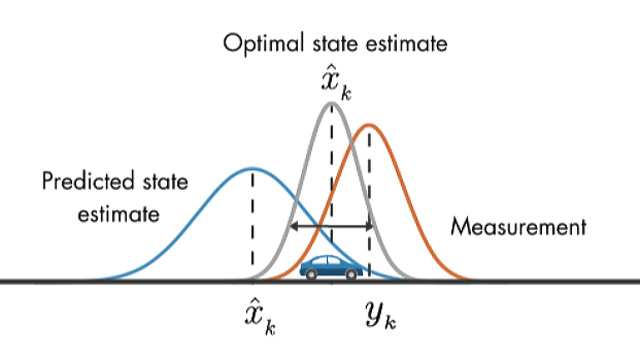
With each new measurement, the “true state” of the object is “predicted”. This happens by applying knowledge about the velocity of the object as of the previous time step to the state. Because there is some uncertainty about the speed and direction that the object traveled since the last timestep (maybe the vehicle turned a corner or slowed down), we add some “noise” to the “true state”.
Next, the “true state” just predicted is modified based on the sensor measurement with an “update”. First, the sensor data is compared against belief about the true state. Next, the “Kalman filter gain”, which is the combination of the uncertainty about the predicted state and the uncertainty of the sensor measurement, is applied to the result, which updates the “true state” to the final belief of the state of the object.
Extended Kalman filters
Because the motion of the object may not be linear; for example, if it accelerates around a curve, or slows down as it exits a highway, or swerves to avoid a bicycle, the model of the object motion may be non-linear. Similarly, the mapping of the sensor observation from the true state space into the observation space may be non-linear, which is the case for radar measurements, which must map distance and angle into location and velocity. As long as the state and measurement models are differentiable functions, the basic Kalman filter can be modified to allow for these situations.
To do this, the basic Kalman filter is “extended” for non-linearity. The extended Kalman filter computations are not significantly different from the basic equations. For this example project, the state and lidar observation models will remain linear, though the radar observation model will be non-linear.
Implementation
Position estimation occurs in a main loop inside the program. First, the program waits for the next sensor measurement, either from the lidar or radar. Lidar sensor measurements contain the absolute position of the vehicle, while radar measurements contain the distance to the vehicle, angle to the vehicle, and speed of the vehicle along the angle. The measurements are passed through the sensor fusion module (which uses a Kalman filter for position estimation), then the new position estimation is compared to ground truth for performance evaluation.
The sensor fusion module encapsulates the core logic for processing a new sensor measurement and updating the estimated state (location and velocity) of the vehicle. Upon initialization, the lidar and radar measurement uncertainties are initialized (which would be provided by the sensor manufacturers), as well as the initial state uncertainty. Upon receiving a first measurement, the initial state is set to the raw measurement from the sensor (using a conversion in the case of a first measurement being from a radar). Next, the model uncertainty is computed based on the elapsed time from the previous measurement, and the “predict” step is run. Finally, the “update” step is run, with small variations depending on the measurement being from a lidar or radar (radar measurements need to be transformed from distance, angle, speed along angle to absolute world coordinates).
The Kalman filter module contains the implementations of the “predict” and “update” steps of the Kalman algorithm. The “predict” step generates a new “true state” and “true state uncertainty” using the state transition model on the current state and current state uncertainty. The “update” step operates differently depending on if running on a lidar or radar measurement. In the case of a lidar measurement, the difference between the raw measurement and the observation model applied to the predicted “true state” is used to generate a state differential. In the case of a radar measurement, the difference between the raw measurement and the “true state” transformed into radar coordinates (distance, angle, speed along angle) is used to generate a state differential. Next, the Kalman filter gain is computed which determines how the new measurement is to be weighted against the “true state”. Finally, the Kalman filter gain is applied to the state differential and added to the “true state” and “true state uncertainty” to update them to their final values.
Performance
To test the sensor fusion using the extended Kalman filter, the simulator provides raw lidar and radar measurements of the vehicle through time. Raw lidar measurements are drawn as red circles, raw radar measurements (transformed into absolute world coordinates) are drawn as blue circles with an arrow pointing in the direction of the observed angle, and sensor fusion vehicle location markers are green triangles.
Clearly, the green position estimation based on the sensor fusion tracks very closely to the vehicle location, even with imprecise measurements from the lidar and radar inputs (both by visual inspection and by the low RMSE.) Success!