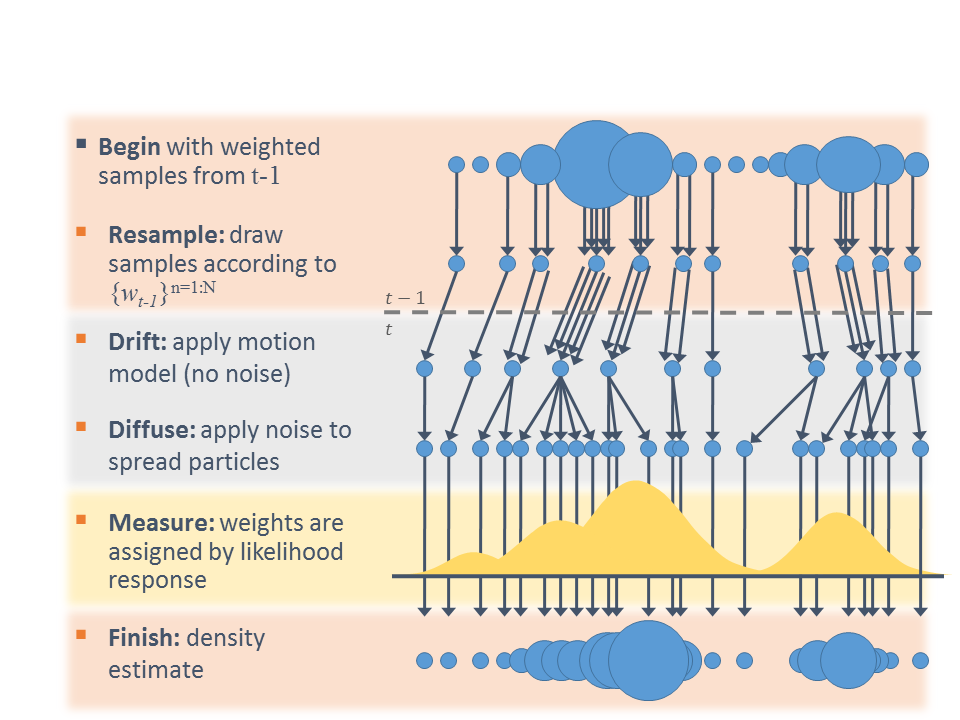
Control systems in autonomous vehicles are used to direct various hardware, including steering wheels, throttle, and brakes among others. These systems take outputs from a path planning system (such as a target velocity in a cruise control) and execute them on the vehicle’s hardware. While humans drivers can easily steer, use the accelerator and brake pedals to safely drive their cars, control systems in autonomous vehicles can be quite challenging to implement for safe, efficient, and pleasant driving.
A Proportional-Integral-Derivative controller, or PID controller for short, is a mechanism which is very common for various applications requiring continuous control changes in autonomous vehicles. By calculating the error between the current and desired value of a control (for example, the angle of the steering wheel), a PID controller applies a correction to smoothly approach the desired value of the control itself.
This repository contains a software system which steers a vehicle around a simulated track using a PID controller. The following techniques are used:
- Apply a PID controller for steering
- Use a training module to implement coordinate descent for PID parameter optimization
Exploring my implementation
All of the code and resources used in this project are available in my Github repository. Enjoy!
Technologies Used
- C++
- uWebSockets
PID Controllers
Many control environments account for both a) a desired setting for a control (such as a target speed in a cruise control or a target vehicle heading from an autonomous vehicle path planner), as well as b) external forces which may change the value of the control (such as a hill or bumpy road which slows down a vehicle’s forward movement). To allow the vehicle to track a target control value, PID controllers repeatedly compute the error between a measurement of a process variable (which contains current value of the control) and the desired setpoint (what the value of the control should be). Then, the controller applies a correction based on the proportional, integral, and derivative parameters of the controller. This allows the vehicle to approach the desired value of the control (such as the target speed) in an efficient way, both quickly and without overshoot.
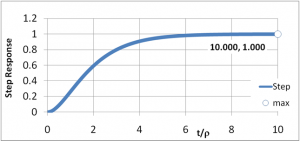
In the image above, the target value of 1 is approached rapidly and smoothly.
The proportional correction adjusts the value of the control in proportion to the difference between the target value and the actual value. For example, if the target speed is 50mph, the proportional correction will be double at a current speed of 40mph (difference of 10mph) than what the correction will be at a current speed of 45mph (difference of 5mph).
The integral correction adjusts the value of the control to account for any constant misalignment between the control output and the hardware. For example, a non-centered steering wheel alignment in vehicles can yield a centered steering wheel which does not guide the vehicle in straight line; the integral correction accounts for this misalignment.
The differential correction adjusts the value of the control to prevent overshooting the target value. Without this, the proportional control would only reduce the control value to zero once the target has been reached; but in true situations, the control value should be reduced to zero to “coast” to the target value in the last moments.
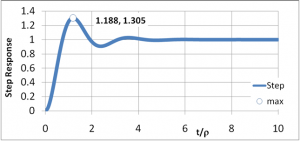
Note how in the image above, the target value of 1 is overshot several times before the actual value settles at the target. A properly adjusted differential correction prevents this.
Implementation
PID controller
The PID controller in this repository is responsible for controlling the steering angle of the vehicle to keep it in the center of the driving lane. To do this, the error used in the PID controller for correction is the cross-track error, which is the distance between the vehicle and the center of the lane. If the vehicle is exactly in the lane center, then the error is zero.
The PID controller for steering is implemented in a standard fashion, with error adjustments based on the sum of:
- current error proportional to a constant (proportional)
- total error summed over each step proportional to a constant (integral)
- error delta since previous step proportional to a constant (differential)
Training module
A training module is implemented to optimize the PID parameters based on the coordinate descent algorithm. The algorithm optimizes each parameter in the error function independently, moving it up or down to find a small improvement in error. This method will find the local minima of the error function overall, meaning that the parameters found are not guaranteed to be the best parameters to minimize error, but will be based on starting parameters given.
The coordinate descent algorithm is embedded in a framework to ensure that the total error measurement for parameter setting ends up taking the entire track into account, not just a small portion of it. However, small portions of track are useful for initial parameter and parameter delta setting in the early moments of the algorithm run, to prevent the vehicle from leaving the drivable portion of the track surface. The training module ensures that if the vehicle appears to be leaving the track surface, the last best parameters are re-installed in the PID controller temporarily, until the vehicle returns to a safe driving state. In that case, those particular parameters that caused the vehicle to lose control are then invalidated as candidates for possible best selection, even if their overall error rate was lower than the previous best error rate.
Results
Using the training module, and with the initial parameters of p = 0.1, i = 0.01, d = 1.0, the training module arrived at a local minima of error with final parameter values p = 0.127777, i = 0.00937592, d = 1.03501 (in the Linux simulator) and p = 0.3011, i = 0.00110, d = 4.8013 (in the Mac simulator). The two simulators provide different data (different vehicle timestep sizes and angles) to the control program; hence, different values are necessary.
The proportional steering control ensures that steering corrections are proportional to the error at each timestep. It is easy to verify this on its own; when the vehicle is travelling away from the center of the lane, the steering commands direct the vehicle back toward the center. However, with this value set and the integral and differential values at zero, the vehicle sways wildely back and forth through the track.
The integral steering control corrects for steering bias of the vehicle. The vehicle naturally “pulls” to the side when the steering command is 0.0; this ensures that the vehicle drives relatively straight when it is in the center of the lane.
The differential steering control attempts to limit the wild sway of the vehicle as it corrects errors by counter-steering. As steering is changed to correct for error, adjustments are reduced by the amount of change between each time step in the simulation. This attempts to prevent the vehicle from overshooting the center of the lane during a correction.
Overall, these settings for the PID controller ensure that the vehicle drives continuously around the track without hitting any road hazards or leaving the drivable portion of the road surface. One caveat is that in the first few seconds of driving, while the vehicle is under 30 mph, the vehicle does sway from side to side.