Autonomous vehicle technology: Model Predictive Control for advanced controls optimization

2017-12-04 Leave a comment

Control systems in autonomous vehicles are used to direct various hardware actuators, including steering wheels, throttle, and brakes among others. These systems take command outputs from a path planning system (such as a target velocity in a cruise control) and execute them on the vehicle’s hardware. While humans drivers can easily steer, use the accelerator and brake pedals to safely drive their cars, control systems in autonomous vehicles can be quite challenging to implement for safe, efficient, and pleasant driving.

One approach to creating a high-quality controller for an autonomous vehicle is to model the vehicle’s dynamics and constraints; this allows for easier analysis and tuning of the controller itself. Model Predictive Control (MPC) is an advanced technique used to control one or more hardware actuators, making optimal control choices for both the present circumstances and the future; for example, when given a trajectory from a path planner. By modeling the dynamics of the vehicle through time, and including explicit constraints on the vehicle dynamics, a MPC can control complex actuators in a much more flexible manner than a PID controller.

This repository contains a software system which implements a MPC for steering and throttle of a vehicle around a simulated track, given a path from a planner.

Exploring my implementation

All of the code and resources used in this project are available in my Github repository. Enjoy!

Technologies Used

C++
uWebSockets
Eigen
C++ Algorithmic Differentiation (CppAD)
Interior Point Optimizer (IPOPT)

Model Predictive Control

Model predictive control shows its strengths when used with moderate to complex systems (like the movement of an autonomous vehicle) that can be linearly modeled or considered approximately linear over a small operating range or timescale.

Vehicle modeling

A basic model for a vehicle is a kinematic model, which captures position, heading, and speed, and ignores many elements like gravity, mass, and tire forces. It is simple and often works well for vehicles moving at low and moderate speeds. Dynamic models can capture a much more rich state of a vehicle such as tire forces, air resistance, gravity, drag, and longitudinal and lateral forces. While dynamic models can more accurately represent how a vehicle moves, basic models have two main advantages: they require less computational resources (making them easier to execute in real-time), and they are transferable between vehicles with different characteristics (such as vehicle mass). A basic kinematic model has simple equations which track how the vehicle state changes with time.

In a vehicle, the main actuators are steering, throttle, and braking. These actuators are limited by their physical designs; they have limitations on the speed at which they can change their values, and they have limits to their values.

Combining the kinematic vehicle model with the actuator constraints form the basis for the MPC used in this repository.

Control creation

Model predictive control restates the problem of following a trajectory from a path planner to an optimization problem using a cost function, whose object is to find the optimal trajectory. In order to develop a controller that works well, a cost function needs to work within the parameters of the model and the constraints. The cost is most generally defined as the difference between where the vehicle is predicted to travel based on the model and where the vehicle is desired to go. A model predictive control implementation simulates actuator inputs, predicting the trajectory as a result of those inputs, and selecting the trajectory with the minimum cost. Once this is complete, the very first set of actuation commands is implemented. This is because the model is only an approximation, and so the trajectory calculated decreases in accuracy far into the future, meaning that the actual trajectory of the vehicle will deviate further and further from the predicted trajectory over time. Finally, the new state of the vehicle is used to feed back into the MPC, starting the process over again.

MPC

Cost functions often include features such as cross-track error (perpendicular distance from the path planner trajectory), heading error (difference between actual heading and desired heading), distance to the destination, difference between speed limit and current speed, and others. Other values can come from control inputs which cause passenger discomfort, such as absolute value of acceleration, jerk (rate of change of acceleration), absolute value of heading difference from a straight path, and change in steering.

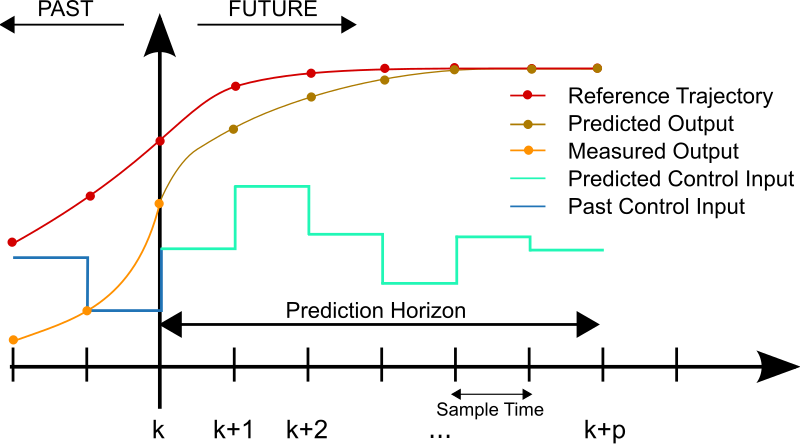
Model predictive controllers predict concrete states several “steps” into the future; the number of steps and the time between steps are controller parameters which are chosen to maximize accuracy and allow for real-time operation of the controller.

With all of these pieces, the model predictive controller runs in a loop, with a polynomial optimizer running at each step to select the best trajectory given the initial model, the model constraints, and the cost function, which returns actuator values in sequence.

Implementation

The Model

The vehicle is modeled using a kinematic bicycle model, consisting of six elements:

vehicle x position (x)
vehicle y position (y)
vehicle heading (psi)
vehicle velocity (v)
cross track error (cte)
vehicle heading error (epsi)

Two actuator values are outputted by the MPC:

steering (steer)
throttle (accel)

The cost function for predictions includes a linear combination of seven components (each component is squared before being used, to ensure differentiability in the cost optimizer):

cross track error
vehicle heading error
difference between current and target speed
steering value (zero being steering straight; multiplied by factor of 2000)
throttle value (zero being no acceleration nor braking)
steering change rate (zero being no change to steering; multiplied by factor of 5)
throttle change rate (zero being no change to throttle; multiplied by factor of 5)

The update equations for each of the states are:

x[t+1] = x[t] + v[t] * cos(psi[t]) * dt
y[t+1] = y[t] + v[t] * sin(psi[t]) * dt
psi[t+1] = psi[t] + v[t] / Lf * steer[t] * dt
v[t+1] = v[t] + accel[t] * dt
cte[t+1] = f(x[t]) - y[t] + v[t] * sin(epsi[t]) * dt
epsi[t+1] = psi[t] - psides[t] + v[t] * steer[t] / Lf * dt

where Lf is a simulation-based constant describing the difference between the front of the vehicle and its center of gravity.

The MPC predicts N state vectors and N-1 actuation vectors using the mathematical optimizer IPOPT. The first actuation vector is used for the each successive actuation of the vehicle (the following actuator values are not used); the state vectors are useful for debugging and visual optimization in the simulator.

Using the cost components above, the vehicle is able to drive smoothly around the simulated track at up to ~55mph without creating hazardous driving conditions.

Timestep length and Elapsed Duration

A timestep length of N = 20 and elapsed duration between timesteps of dt = 0.05 was initially chosen. However, it was found that this dt led to steering overcorrection of the vehicle, so the dt was doubled to 0.1 and N halved to 10. After that, the total length of the predicted course was found to be too short, with too many back and forth steering corrections. By increasing the N = 20, the vehicle was able to drive around the path with enough future predicted states while not predicting sharp corrections.

Polynomial fitting and MPC pre-processing

Waypoints from the simulator are received in map coordinates; before they can be used, they are converted to vehicle coordinates (using the map coordinates of the vehicle itself). These waypoints (now in vehicle coordinates) are then used to fit a 3rd degree polynomial. This polynomial is used to compute the desired location of the vehicle on the path; this allows for computing the cross track error as the distance between the desired location of the vehicle and the current location and the vehicle heading error.

Model Predictive Control with Latency

Due to a 100ms simulated actuator delay between actuator value computation and actuator implementation, any actuator values computed by the MPC are 100ms out of date by the time they arrive at the simulated vehicle. This reflects reality of true vehicle hardware. Because of this, a latency adjustment is computed which, at each actuator computation, predicts the vehicle state into the future by the latency amount. This is done simply by using the same vehicle update equations above a single time before passing the state into the MPC itself.

With these adjustments, the MPC that was implemented easily handles a 100ms latency with the simulated vehicle driving at ~55mph.

Results

The simulated vehicle drives around the track with minimal steering jerk and no sudden acceleration or deceleration. Note that the steering is much smoother than my PID controller implementation, which operates on optimizing for zero cross-track error alone.

In the video, the yellow line is a polynomial fit of the yellow line dots, which are input targets from the path planner. The green line is a polynomial fit of the green line dots, which track the optimal trajectory as determined by the MPC.

Autonomous Vehicle Projects: PID Control for Vehicle Steering

2017-11-28 Leave a comment

Control systems in autonomous vehicles are used to direct various hardware, including steering wheels, throttle, and brakes among others. These systems take outputs from a path planning system (such as a target velocity in a cruise control) and execute them on the vehicle’s hardware. While humans drivers can easily steer, use the accelerator and brake pedals to safely drive their cars, control systems in autonomous vehicles can be quite challenging to implement for safe, efficient, and pleasant driving.

A Proportional-Integral-Derivative controller, or PID controller for short, is a mechanism which is very common for various applications requiring continuous control changes in autonomous vehicles. By calculating the error between the current and desired value of a control (for example, the angle of the steering wheel), a PID controller applies a correction to smoothly approach the desired value of the control itself.

This repository contains a software system which steers a vehicle around a simulated track using a PID controller. The following techniques are used:

Apply a PID controller for steering
Use a training module to implement coordinate descent for PID parameter optimization

Exploring my implementation

All of the code and resources used in this project are available in my Github repository. Enjoy!

Technologies Used

C++
uWebSockets

PID Controllers

Many control environments account for both a) a desired setting for a control (such as a target speed in a cruise control or a target vehicle heading from an autonomous vehicle path planner), as well as b) external forces which may change the value of the control (such as a hill or bumpy road which slows down a vehicle’s forward movement). To allow the vehicle to track a target control value, PID controllers repeatedly compute the error between a measurement of a process variable (which contains current value of the control) and the desired setpoint (what the value of the control should be). Then, the controller applies a correction based on the proportional, integral, and derivative parameters of the controller. This allows the vehicle to approach the desired value of the control (such as the target speed) in an efficient way, both quickly and without overshoot.

PID smooth

In the image above, the target value of 1 is approached rapidly and smoothly.

The proportional correction adjusts the value of the control in proportion to the difference between the target value and the actual value. For example, if the target speed is 50mph, the proportional correction will be double at a current speed of 40mph (difference of 10mph) than what the correction will be at a current speed of 45mph (difference of 5mph).

The integral correction adjusts the value of the control to account for any constant misalignment between the control output and the hardware. For example, a non-centered steering wheel alignment in vehicles can yield a centered steering wheel which does not guide the vehicle in straight line; the integral correction accounts for this misalignment.

The differential correction adjusts the value of the control to prevent overshooting the target value. Without this, the proportional control would only reduce the control value to zero once the target has been reached; but in true situations, the control value should be reduced to zero to “coast” to the target value in the last moments.

PID overshoot

Note how in the image above, the target value of 1 is overshot several times before the actual value settles at the target. A properly adjusted differential correction prevents this.

Implementation

PID controller

The PID controller in this repository is responsible for controlling the steering angle of the vehicle to keep it in the center of the driving lane. To do this, the error used in the PID controller for correction is the cross-track error, which is the distance between the vehicle and the center of the lane. If the vehicle is exactly in the lane center, then the error is zero.

The PID controller for steering is implemented in a standard fashion, with error adjustments based on the sum of:

current error proportional to a constant (proportional)
total error summed over each step proportional to a constant (integral)
error delta since previous step proportional to a constant (differential)

Training module

A training module is implemented to optimize the PID parameters based on the coordinate descent algorithm. The algorithm optimizes each parameter in the error function independently, moving it up or down to find a small improvement in error. This method will find the local minima of the error function overall, meaning that the parameters found are not guaranteed to be the best parameters to minimize error, but will be based on starting parameters given.

The coordinate descent algorithm is embedded in a framework to ensure that the total error measurement for parameter setting ends up taking the entire track into account, not just a small portion of it. However, small portions of track are useful for initial parameter and parameter delta setting in the early moments of the algorithm run, to prevent the vehicle from leaving the drivable portion of the track surface. The training module ensures that if the vehicle appears to be leaving the track surface, the last best parameters are re-installed in the PID controller temporarily, until the vehicle returns to a safe driving state. In that case, those particular parameters that caused the vehicle to lose control are then invalidated as candidates for possible best selection, even if their overall error rate was lower than the previous best error rate.

Results

Using the training module, and with the initial parameters of p = 0.1, i = 0.01, d = 1.0, the training module arrived at a local minima of error with final parameter values p = 0.127777, i = 0.00937592, d = 1.03501 (in the Linux simulator) and p = 0.3011, i = 0.00110, d = 4.8013 (in the Mac simulator). The two simulators provide different data (different vehicle timestep sizes and angles) to the control program; hence, different values are necessary.

The proportional steering control ensures that steering corrections are proportional to the error at each timestep. It is easy to verify this on its own; when the vehicle is travelling away from the center of the lane, the steering commands direct the vehicle back toward the center. However, with this value set and the integral and differential values at zero, the vehicle sways wildely back and forth through the track.

The integral steering control corrects for steering bias of the vehicle. The vehicle naturally “pulls” to the side when the steering command is 0.0; this ensures that the vehicle drives relatively straight when it is in the center of the lane.

The differential steering control attempts to limit the wild sway of the vehicle as it corrects errors by counter-steering. As steering is changed to correct for error, adjustments are reduced by the amount of change between each time step in the simulation. This attempts to prevent the vehicle from overshooting the center of the lane during a correction.

Overall, these settings for the PID controller ensure that the vehicle drives continuously around the track without hitting any road hazards or leaving the drivable portion of the road surface. One caveat is that in the first few seconds of driving, while the vehicle is under 30 mph, the vehicle does sway from side to side.

Autonomous Vehicle Technology: Localization using Particle Filters

2017-11-08 Leave a comment

In order to drive safely, autonomous vehicles on public roads need to know where they are in the world. Tasks easy for humans, such as staying in driving lanes at all times, would be impossible for an autonomous vehicle to perform without highly accurate vehicle location information. Determining the vehicle’s location in the world is called localization. One popular and well-known localization system is the global positioning system (GPS), which can provide rough localization; it often has accuracy of one to three meters, but the accuracy can decrease to upwards of fifty meters with poor line off sight to the sky or other interference. Unfortunately, this is not accurate enough for an autonomous vehicle; a localization accuracy of under ten centimeters is considered the upper limit for safe driving.

Like the techniques involved in object tracking using extended and unscented Kalman filters, localization techniques are often probabilistic. The unscented Kalman filter is flexible enough for many object tracking applications; however, when even higher accuracy is required for vehicle localization, another technique can be used: a particle filter.

Exploring my implementation

All of the code and resources used in this project are available in my Github repository. Enjoy!

Technologies Used

C++
uWebSocketIO

Particle Filters

Particle filters are similar to unscented Kalman filters in that they update the state of an object (for example, the location and orientation) by transforming a set of points through a function to predict a future state, given noisy and partial observations of the world. However, unlike unscented Kalman filters, particle filters may choose points to transform at random, rather than from a Gaussian distribution. This eliminates the need to assume a static state motion or measurement model. The number of points required for a particle filter to obtain the same level of accuracy as an unscented Kalman filter is generally higher, which makes a particle filter more computationally complex and memory intensive. Additionally, there is a choice to be made regarding the number of particles included in the filter (the time complexity of computing the algorithm is linear in the number of particles). However, particle filters do converge to the true state of the object being predicted as number of particles increases, unlike unscented Kalman filters, which have no such convergence properties.

Particle filter steps

In a particle filter, the points, or “particles”, are chosen to represent concrete guesses as to the actual state being predicted. At each time step, particles are randomly sampled from the state space. The probability of a particle being chosen is proportional to the probablility of it being the correct state, given the sensor measurements seen so far. The update step in a particle filter can be seen as selecting the most likely hypotheses among the set of guessed states; as more sensor measurements become available, those more likely to be true are kept, while those less likely are removed.

Particle filters for localization

When used for localization, particle filters become a particularly effective technique. Because they can approximate non-parametric functions, they perform better in many non-linear model environments, including situations with multiple possible localization positions. For example, when using a Kalman filter (extended or unscented), a vehicle driving down a road with many similar lampposts may decide that it is next to a lamppost, but may have trouble determining which lamppost it is next to.

In using a particle filter for localization, data from onboard sensors (such as radar and lidar) can be used to measure distances to static objects (trees, poles, walls), which may involve sensor fusion. With a pre-loaded map which has trusted coordinates of these fixed objects, a particle filter matches observations of objects in the world against those in the map, and then determines where the vehicle is in the map space. To start, particles may initially be chosen at random from all locations, with no assumptions about where the vehicle is. However, in practice, some sort of one-time hint about the general location from GPS may be provided. At each time step, the algorithm uses its previous belief about vehicle location, the current vehicle control values, and sensor measurements, and outputs a new belief about the vehicle location.

The algorithm runs by updating the current set of particles (possible locations) according to the vehicle control command, simulating motion of all of the particles. For instance, if the vehicle is travelling forward, all particles move forward. If the vehicle turns to the right, all of the particles turn to the right. Because the result of a control does not always complete as expected, some amount of noise is added to the particle movement to simulate this uncertainty. Each particle is then considered to be the possible location of the vehicle, and the probability that the location is the true location of the vehicle given the current sensor measurements is computed. Those probabilities are used as weights to randomly select new particles from the previous particle list. Because of this, particles which are consistent with sensor measurements are more likely to be chosen (and may even be chosen more than once!), and particles which are inconsisent with the measurements are less likely to be chosen. However, to prevent convergence on an incorrect location (if the vehicle is stationary, for instance), extra uniformly sampled particles can be added.

With every iteration of the particle filter algorithm, the selected particles converge to the true location of the vehicle, which makes intuitive sense: as the vehicle senses more of its environment, it should be expected to become increasingly sure of its position.

Localization maze

Implementation

The localization algorithm exists as a loop, where new sensor measurements and control commands are read. On the first sensor measurement, the particle filter is initialized with that measurement; on subsequent measurements, the particle filter is run to predict the new location of the vehicle. Next, the particles have their weights updated using observations from sensors and known map landmarks, then particles are resampled. Finally, the particle with the highest weight is chosen as the new location of the vehicle.

Inside the particle filter, the initialization step creates 100 particles, locates them all at the first measurement, and then adjusts each particle randomly according to the sensor measurement uncertainty distribution. During prediction, each particle’s next location is predicted by moving it according to the velocity and turn rate from most recent vehicle control command.

To update the weights for each particle based on the sensor observations of landmarks, the landmarks nearest the particle are chosen. Next, each observation is paired with its closest true landmark. Finally, the particle’s weight is set to the product of the distance between each true landmark and its closest observation.

Particle resampling occurs according to the particles weights, which is a standard sampling with replacement approach.

Performance

To test the localization using the particle filter, the simulator provides sensor measurements of fixed objects in the world. These are plotted in the simulator as black crosses with circles around them. Green lines drawn between the vehicle and the circles indicate fixed objects which are being tracked.

The jitter between the vehicle (true location) and the grey circle (predicted location) is kept to a relative minimum over time, even during accelerations, decelerations, and turns. This indicates that the filter does a relatively good job at localization.

Autonomous Vehicle Technology: Sensor Fusion and Unscented Kalman Filters for Object Tracking

2017-10-17 Leave a comment

While cameras are incredibly useful for autonomous vehicles (such as in traffic sign detection and classification), other sensors also provide invaluable data for creating a complete picture of the environment around a vehicle. Because different sensors have different capabilities, using multiple sensors simultaneously can yield a more accurate picture of the world than using one sensor alone. Sensor fusion is this technique of combining data from multiple sensors. Two frequently used non-camera-based sensor technologies used in autonomous vehicles are radar and lidar, which have different strengths and weaknesses and produce very different output data.

Radars exist in many different forms in a vehicle: for use in adaptive cruise control, blind spot warning, collision warning, collision avoidance, to name a few. Radar uses the Doppler effect to measure speed and angle to a target. Radar waves reflect off hard surfaces, but can pass through fog and rain, have a wide field of view and a long range. However, their resolution is poor compared to lidar or cameras, and they can pick up radar clutter from small objects with high reflectivity. Lidars use infrared laser beams to determine the exact location of a target. Lidar data resolution is higher than radar, but lidars cannot measure the velocity of objects, and they are more adversely affected by fog and rain.

Lidar point cloud

Example of lidar point cloud

Radar map and velocity

Example of radar location and velocity data

A very popular mechanism for object tracking in autonomous vehicles is a Kalman filter. Kalman filters uses multiple imprecise measurements over time to estimate locations of objects, which is more accurate than single measurements alone. This is possible by iterating between estimating the object state and uncertainty, and updating the state and uncertainty with a new weighted measurement, with more weight being given to measurements with higher precision. This works great for linear models, but for non-linear models (such as those which involve a turning car, a bicycle, or a radar measurement), the extended Kalman filter must be used. Extended Kalman filters are considered the standard for many autonomous vehicle tracking systems.

Unfortunately, when the models are very non-linear, the extended Kalman filter can yield very poor performance. As a remedy, the unscented Kalman filter can be used.

Kalman filter joint probability

Exploring my implementation

All of the code and resources used in this project are available in my Github repository. Enjoy!

Technologies Used

C++
uWebSockets

Kalman filters

Conceptually, Kalman filters work on the assumption that the actual or “true” state of the object (for instance, location and velocity) and the “true” uncertainty of the state may not be knowable. Rather, by using previous estimates about the object’s state, knowledge of how the object’s state changes (what direction it is headed and how fast), uncertainty about the movement of the vehicle, the measurement from sensors, and uncertainty about sensor measurements, an estimate of the object’s state can be computed which is more accurate than just assuming the values from raw sensor measurements.

Kalman filter algorithm

With each new measurement, the “true state” of the object is “predicted”. This happens by applying knowledge about the velocity of the object as of the previous time step to the state. Because there is some uncertainty about the speed and direction that the object traveled since the last timestep (maybe the vehicle turned a corner or slowed down), we add some “noise” to the “true state”.

Next, the “true state” just predicted is modified based on the sensor measurement with an “update”. First, the sensor data is compared against belief about the true state. Next, the “Kalman filter gain”, which is the combination of the uncertainty about the predicted state and the uncertainty of the sensor measurement, is applied to the result, which updates the “true state” to the final belief of the state of the object.

Unscented Kalman filters

Because the motion of the object may not be linear; for example, if it accelerates around a curve, or slows down as it exits a highway, or swerves to avoid a bicycle, the model of the object motion may be non-linear. Similarly, the mapping of the sensor observation from the true state space into the observation space may be non-linear, which is the case for radar measurements, which must map distance and angle into location and velocity. The extended Kalman filter can often be used here when the non-linear motion or observation models are easily differentiable and can be approximated by a linear functions.

However, in some cases the motion or observation models are either not easily differentiable or cannot be easily approximated by linear functions. For example, many motion models use non-constant velocity; often they include both straight lines and turns. Even if these functions could be differentiated properly, the probability distributions of the uncertainty in the models might not be normally distributed after a “predict” or “update” step, which breaks the Kalman filter assumptions. To avoid this problem, using an unscented Kalman filter can be used, which involves transforming point samples from a Gaussian distribution through the non-linear models to approximate the final probability distribution. This has two main advantages:

* the sample points often approximate the probability distribution of the non-linear functions better than a linear model does

* a Jacobian matrix is not necessary to compute

In order to preserve the “normal” nature of the motion and observation probability distributions, the unscented Kalman filter uses the “unscented transformation” to map a set of points through the motion and observation models. To do this, a group of “sigma points” are selected which represent the original state probability distribution. Once transformed by the non-linear model, the mean and per-dimensional standard deviations of the transformed points are computed, which yields a useful approximation of the real mean and standard deviation of the non-linear model.

Other than using sigma points to represent the motion and observation model probability functions, the unscented Kalman filter flow is similar to that of the extended Kalman filter, including a measurement-model independent “predict” step, followed by a measurement-model dependent “update” step.

Implementation

Position estimation occurs in a main loop inside the program. First, the program waits for the next sensor measurement, either from the lidar or radar. Lidar sensor measurements contain the absolute position of the vehicle, while radar measurements contain the distance to the vehicle, angle to the vehicle, and speed of the vehicle along the angle. The measurements are passed through the sensor fusion module (which uses a Kalman filter for position estimation), then the new position estimation is compared to ground truth for performance evaluation.

The unscented Kalman filter module encapsulates the core logic for processing a new sensor measurement and updating the estimated state (location and velocity) of the vehicle. Upon initialization, the lidar and radar measurement uncertainties are initialized (which would be provided by the sensor manufacturers), as well as the motion model uncertainty. Upon receiving a first measurement, the initial state is set to the raw measurement from the sensor (using a conversion in the case of the first measurement being from a radar). Next, the “predict” and “update” steps are run.

The “predict” step has three main functions:

generating sigma points
predicting the sigma points through the motion model transform
predicting the new state mean and covariances

There are two different “update” implementations; one for radar and one for lidar. Both implementations must first transform the predicted sigma points into the measurement space, then update the predicted state based on the transformed measurements.

Performance

To test the sensor fusion using the unscented Kalman filter, the simulator provides raw lidar and radar measurements of the vehicle through time. Raw lidar measurements are drawn as red circles, raw radar measurements (transformed into absolute world coordinates) are drawn as blue circles with an arrow pointing in the direction of the observed angle, and sensor fusion vehicle location markers are green triangles.

Clearly, the green position estimation based on the sensor fusion tracks very closely to the vehicle location, even with imprecise measurements from the lidar and radar inputs (both by visual inspection and by the low RMSE.)

Additionally, by comparison with the extended Kalman filter on the same input dataset, it is clear that the error in the estimated positions from the unscented Kalman filter are lower than that of the extended Kalman filter:

	Extended	Unscented	Reduction in Error
PX	0.0974	0.0756	22%
PY	0.0855	0.0849	1%
VX	0.4517	0.3530	22%
PY	0.4404	0.2428	45%